Our curiosity about the fundamental nature of the Universe on large scales provides much of the motivation for the SDSS. Here we outline how the size, uniformity, and completeness of this survey will enable us to characterize large scale structure at the present epoch.
Observations of the cosmic microwave background tell us that the early Universe was homogeneous, but we observe today's Universe to be highly structured over a vast range of scales, from planets to superclusters. The goal of studying large scale structure is to understand the transition from a Universe filled smoothly with hot plasma to one filled with galaxies, clusters, and superclusters. The leading hypothesis is that gravitational instability amplified small fluctuations present at recombination into the structures that we observe today. There are various ways to state the field's "big questions", but any complete list would include the following. Is the gravitational instability explanation basically correct? If so, what were the properties of the primordial fluctuations, and what physical process created them? What is the dark matter? What are the values of the density parameter, Omega, and the cosmological constant, Lambda? The answers to these questions are intimately linked to theories of particle physics, and to theories of the origin, early history, and ultimate fate of the Universe. Cosmology thus offers an indirect glimpse of physics at energies that can never be reached in terrestrial experiments.
In addition to these "fundamental" questions, there is a second category of important, "astrophysical" questions, related to galaxy formation. How did galaxies form? What physical processes, besides gravity, played an important role? What processes determine galaxy luminosity, size, color, and morphology? What is the relation between the distribution of galaxies and the underlying distribution of mass? Because galaxies are the markers by which we trace large scale structure, we cannot address the first category of questions without simultaneously addressing the second, especially the final question about the relation between galaxies and mass.
Several factors will make the SDSS a uniquely powerful database for answering these questions. One is the sheer number of galaxies in the redshift sample, a nearly two-order-of-magnitude increase over the largest existing surveys. Another is the quality and uniformity of the photometric data that will be used to select spectroscopic targets and measure Galactic extinction; these will give superb control over systematic effects that might otherwise limit the accuracy of clustering analyses on large scales. The photometric data and moderate-resolution galaxy spectra also allow one to classify the galaxies of the redshift sample in a variety of ways, making it possible to study the relative clustering of different galaxy types. Finally, while the 1,000,000 galaxy redshift sample is perhaps the most visible element of the SDSS, at least from the point of view of large scale structure, the deeper, multi-color, photometric survey and the spectroscopic survey of quasars and their absorption systems will also make major contributions to our understanding of galaxy and structure formation. Together these features of the SDSS will bring unprecedented precision, dynamic range, and detail to the study of structure in the Universe.
The design of the SDSS redshift survey is crucial to its effectiveness as a tool for studying large scale structure. The goal of this survey is not to measure a single statistical property of the distribution of galaxies, such as the power spectrum of density fluctuations, or the maximum size of non-linear structures. Instead, we desire an accurate description of the galaxy distribution over a wide range of physical scales, in order to address the questions listed above. To meet this goal, we plan to do a wide-angle, deep redshift survey which fully samples the galaxy distribution (cf. Chapter 1). In the remainder of this subsection, we describe the scientific motivation for this approach, and in Sections 3.1.3 and 3.1.4 we discuss ways of using the SDSS data to measure cosmological parameters and test theories of structure formation.
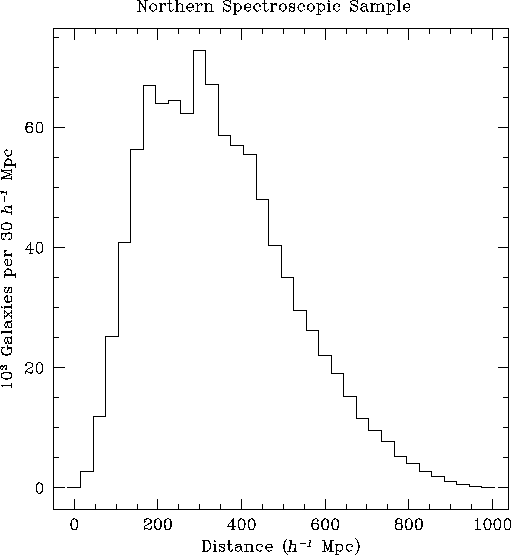
Figure 3.1.1 shows the volume of the redshift survey in schematic form: the upper cone is the Northern survey, while the three narrow fans below are the Southern stripes (see Section 5.5 and below). Figures 3.1.2 and 3.1.3 display two views of a simulated SDSS spectroscopic sample, drawn from a large N-body simulation of a low-density, cold dark matter Universe. Details of the simulation are given in Chapter 13. For these simulations, the spectroscopic sample consisted of all galaxies with apparent magnitude r'<17.55 and apparent half-light diameter greater than 2 arcseconds, selecting just under one million galaxies over the survey area. Since the time that this simulation was done, the details of the galaxy selection criteria have changed; see below, but the qualitative nature of this figure is not sensitively dependent on these details. Figure 3.1.2 shows the distribution of this Northern spectroscopic sample on the sky. We have plotted only half of the points, selected at random, so as not to blacken the page completely. Figure 3.1.3 shows the distribution of galaxies in redshift space in a 6° by 130° slice along the survey equator, which contains about 6% of the spectroscopic sample. Figure 3.1.4 shows the redshift histogram of the sample galaxies. The median depth of the sample is ~ 300 h-1 Mpc , and there is useful information on the density field to ~ 600 h-1 Mpc , with a few galaxies as far away as 1000 h-1 Mpc .

A schematic representation of the survey geometry. The upper cone is the Northern spectroscopic survey over a large solid angle, while the three thin fans below it are the Southern survey.

The distribution on the sky of a simulated catalog. This is for the Northern spectroscopic sample, drawn from a large N-body calculation. The survey footprint is a 130° x 110° ellipse, shown in equal-area projection. We have randomly removed half of the points to reduce crowding. Details of the simulation are described in Chapter 13.

A few examples from the recent history of redshift surveys illustrate how the detection of structure depends on both the survey geometry and the sampling rate. Observing in narrow pencil beams in the direction of the constellation Boötes, Kirshner et al. (1981) detected a 60 h-1 Mpc diameter void in the galaxy distribution. The geometry and sampling of the Kirshner et al. survey was well suited to detection of a single void, but it could not answer the question of how common such structures are. De Lapparent, Geller and Huchra (1986, hereafter CfA2) measured redshifts of a magnitude-limited sample of galaxies in a narrow strip on the sky, and found that (1) large voids fill most of the volume of space and (2) these voids are surrounded by thin, dense, coherent structures. Demonstration of the first result was possible because of the geometry and depth of the survey, demonstration of the second because of the dense sampling. There were hints of this structure in the shallower survey of the same region by Huchra et al. (1983), but the deeper CfA2 sample was required to reveal the structure clearly. Sparse samples of the galaxy distribution, e.g. the QDOT (Saunders et al. 1991) survey of one in six IRAS galaxies, have provided useful statistical measures of low-order clustering on large scales, but sparse surveys have less power to detect coherent overdense and underdense regions. Perhaps because of this limitation, members of the QDOT team have elected to follow up their one-in-six survey by obtaining a complete (one-in-one) survey of IRAS galaxies to the same limiting flux, now nearing completion.
In order to encompass a fair sample of the Universe, a redshift survey must sample a very large volume. We do not know a priori how large such a volume must be, but existing observations provide the minimum constraints. Our picture of the geometry and size of existing structures became clearer as the CfA2 survey was extended over a larger solid angle (e.g. Vogeley et al. 1994). The largest of the structures found is a dense region measuring 150 h-1 Mpc by 50 h-1 Mpc -- the "Great Wall" (Geller and Huchra 1989). Giovanelli et al. (1986) find a similar coherent structure in a complete redshift survey of the Perseus-Pisces region, and da Costa et al. (1988) find another such "wall" in the Southern hemisphere (cf. Santiago et al. 1996). However, none of these surveys covers a large enough volume to investigate the frequency of these structures. In quantitative terms, the observed power spectrum of galaxy density fluctuations continues to rise on scales up to >~ 100 h-1 Mpc (Vogeley et al. 1992; Loveday et al. 1992; Fisher et al. 1993; Feldman et al. 1994; Park et al. 1994; Baugh and Efstathiou 1993; Peacock and Dodds 1994; da Costa et al. 1994; Landy et al. 1996; cf. the review by Strauss and Willick 1995). The observed power spectrum may be influenced by these few, largest, nearby structures. Thus a fair sample clearly must include many volumes with scale ~ 100 h-1 Mpc .
The sampling rate and geometry of a survey can strongly influence the largest structures seen. A very deep pencil-beam survey by Broadhurst et al. (1990, hereafter BEKS) showed remarkable clustering signatures on a scale of 128 h-1 Mpc . First results from the redshift survey of Shectman et al. (1996, hereafter LC for the Las Campanas survey), has found evidence for an excess of power on similar scales (Landy et al. 1996). The LC survey covers a two narrow wedges in the Southern sky; it is deeper than CfA2 but less deep than the BEKS survey. While different survey geometries are appropriate for elucidating different features of large scale structure, a deep survey with a large opening angle and full sampling of the galaxy population is the only way to get a complete picture of the galaxy distribution. Coverage of the whole sky is extremely helpful if one wants to compare velocity and density fields in the nearby Universe, and redshift surveys of infrared-selected galaxies (Strauss et al. 1992; Fisher et al. 1995; Lawrence et al. 1995) are invaluable for this purpose. However, these surveys are much shallower than the SDSS, with almost two orders of magnitude fewer galaxies, so they are not nearly as powerful for statistical analyses of clustering.

A schematic three-dimensional comparison of window functions. The window function is the Fourier transform of the survey volume; it can be thought of as the point-spread function for measurements of the galaxy power spectrum. The narrower the window function, the better the sensitivity to large scale clustering. Surveys with highly anisotropic shapes (slices, pencil beams) have highly anisotropic window functions; as a result, estimates of large scale clustering can be polluted by aliased power from small scales. The window functions of five surveys are shown here: lower left is QDOT, upper left is CfA2, upper right is LC, lower right is the BEKS survey, and the small dot in the center is the SDSS.
Our ability to constrain the fluctuation spectrum on scales approaching those examined by CMB anisotropy measurements depends on both the total volume and the shape of the survey. An important feature of the SDSS redshift survey is the "window function" with which it will observe the Universe. A slice or pencil-beam geometry samples many independent volumes with a smaller number of galaxies, but the small extent in one or two dimensions makes the fluctuation spectrum computed for such surveys strongly affected by aliasing (cf. Kaiser and Peacock 1991; Tegmark 1995). In other words, strong clustering on small scales may overwhelm the true signal on much larger scales. The SDSS redshift survey volume is large enough to include many independent structures on the scale of the "Great Wall," and has both sufficient angular coverage and depth to ensure that measurement of the fluctuation spectrum on scales of a few hundred h-1 Mpc is not strongly affected by aliasing. The redshift survey in the South Galactic cap will further help by nearly doubling the largest baseline in the survey. Indeed, we plan to do galaxy spectroscopy in three stripes in the South (Fig. 3.1.1), along great circles centered at alpha = 0h, delta = 0°, alpha = 0h, delta = +15°, and alpha = 0h, delta = -10°. This maximizes the number of independent measures of the longest baselines. In Figure 3.1.5 we provide a schematic representation of the window function in the Fourier domain for the SDSS and several current surveys. Figure 3.1.6 shows the window functions more quantitatively. The quantity plotted is the mean square of the window function as a function of k (averaged over direction), and normalized to unity at k = 0 . Also plotted is the window function for the CfA2 survey (Park et al. 1994), which represents the current state of the art; the tremendous improvement of the SDSS over the CfA2 for measuring the power spectrum on large scales with high resolution in k -space is immediately apparent.
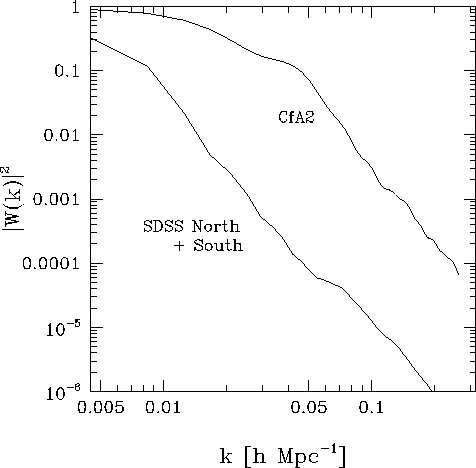
The Fourier window function of a volume-limited sample. The function is shown for the SDSS galaxy redshift survey ( Rmax=500h-1 Mpc), including the main North Galactic Cap survey and three stripes in the South, compared to the window function for the full CfA2 Redshift Survey ( Rmax=130h-1 Mpc; cf., Park et al. 1994). The observed power spectrum is a convolution of the true power spectrum with this function. To reveal the relative sharpness of the window functions, the normalization in this figure is such that |W(k=0)|21 .
A key element of the strategy for the SDSS redshift survey is full sampling of the galaxy distribution. For some specific instrumental set-ups, specific models of the galaxy distribution, and specific, low-order measures of large scale clustering, one can gain efficiency by sparse sampling, i.e. by observing only a fraction of the galaxies down to some limiting magnitude. However, we do not know the properties of the large scale distribution of galaxies a priori, and we want the flexibility to measure a wide range of clustering statistics from the data, including statistics that characterize higher-order clustering. In this case, there is no better strategy than simply observing all galaxies; any attempt to "optimize" in other ways would depend strongly on our presumptions about the the statistical properties and the topology of the large scale galaxy distribution. The design of the SDSS telescope itself (in particular, the field of view and the number of fibers in the spectrograph) has been affected by these considerations.
If fluctuations in the Universe are strictly Gaussian, their full statistical description is contained in the two-point correlation function or in its Fourier transform, the power spectrum. The phases of the individual Fourier components are random for such a process, and all higher-order measures of clustering vanish. In this case, Kaiser (1986) shows that measuring the redshifts of a small fraction of the galaxies is the most efficient way to measure the power spectrum on large scales, for a given amount of telescope time, and for a single-object spectrograph. However, given the field of view and number of fibers in our spectrograph, we will be able to observe essentially all the galaxies in a given field to the faintest magnitude for which we can measure redshifts in a reasonable amount of time. With the SDSS instrumentation, therefore, there would be no gains in efficiency by sparse sampling. Moreover, if the Universe contains sharp large scale features like the "Great Wall", a sparsely sampled survey may fail to identify them because it is less sensitive to the higher-order correlations (equivalently, the phase correlations) that characterize such structures. A distribution with high-order clustering can be very different from a homogeneous, isotropic, Gaussian random field with the same second-order statistical properties. We demonstrate this with a simple but graphic example in Figure 3.1.7, which shows a pair of two-dimensional distributions with the same two-point correlation functions. One of these has very non-random phases, while the phases in the other have been randomized. A sparse survey designed only to measure the two-point correlation function would miss the very real differences between these two distributions.
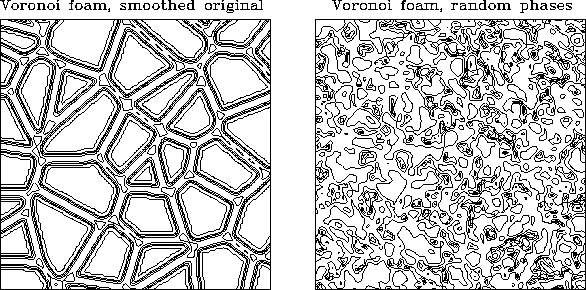
Two distributions with the same correlation function. The left-hand figure is a two-dimensional Voronoi foam, generated by the median surfaces between Poisson "seeds" at a mean separation of 100 h-1 Mpc . In this simple toy model, galaxies reside only on the walls of the foam, smoothed to give the walls a finite thickness. The structure has a well defined second-order statistic, but it also has correlated phases. This picture has been Fourier transformed, all the phases randomized, then transformed back again. The result is another two-dimensional density plot, shown on the right hand side, with the same second-order properties, but with a Gaussian density distribution function.
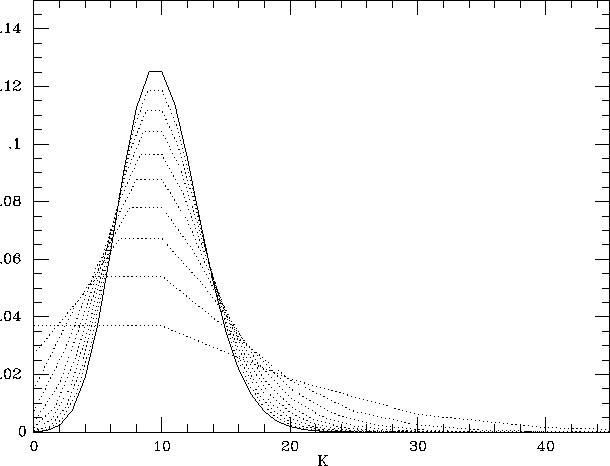
Sparse sampling can severely compromise one's ability to recover the underlying galaxy density field (cf. de Lapparent et al. 1991; Ramella et al. 1990). Figure 3.1.8 illustrates this point with a simple example (cf., Szapudi and Szalay 1995). Suppose that we are interested in the distribution of galaxy counts in cells that contain, on average, 10 galaxies above the survey magnitude limit. We assume that the underlying distribution of galaxy counts N is a Poisson distribution with a mean of 10. The solid line in the left-hand panel shows this distribution. Now suppose that we observe the galaxy distribution with a sampling rate p<1 . The number of galaxies M detected in a cell that actually contains N galaxies will have a binomial distribution

The unbiased estimator for the true number of galaxies in the cell is simply K=M/p . The dotted lines in the left-hand panel show the distribution of inferred counts K for sampling rates p=0.9, 0.8, 0.7, ... , 0.1. This distribution is
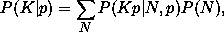
where P(Kp | N,p) is the binomial distribution given above and P(N) is a Poisson distribution of mean 10. At p=0.9 the distribution of inferred counts is quite close to the true distribution, but as the sampling rate decreases the distribution of inferred counts becomes very broad. The right-hand panel shows a logarithmic plot of the cumulative distribution, the number of cells with inferred counts exceeding a value K . For large values of K , the curves for low sampling rates exceed the true curve by orders of magnitude. To some extent one can correct estimates of statistical quantities for finite sampling (cf., Colombi, Bouchet, and Schaeffer 1994, 1995), but when the sampling rate is low even a corrected estimate can have large random errors and systematic biases that are sensitive to a priori assumptions about the clustering. Furthermore, as Figure 3.1.8 makes clear, it can become virtually impossible to infer the actual galaxy density field -- the true number of galaxies in each spatial cell -- because sparse sampling leaves only a tenuous connection between the number of galaxies present and the number actually observed.
Low sampling rates seriously jeopardize the ability to recover information about the galaxy distribution beyond second-order clustering statistics. By obtaining a full sample, the SDSS will produce a data set that is well suited to a wide range of analyses aimed at a wide range of questions, including ones that have not yet been formulated. The design of the imaging and spectroscopic systems allows this full sampling to be obtained without loss of efficiency.
Simply saying that we will select for spectroscopic observation the brightest million galaxies in the survey area is not adequate. There are many ways in which to measure magnitudes for extended galaxies; we must also specify in which band or bands the galaxy selection is to be done. The selection criteria must be simple, and robust. They must target the full range of galaxy types, and must give a high probability of actually being able to measure a redshift. We must have selection criteria such that the efficiency of identifying the right spectroscopic targets (e.g. separating galaxies from stars) and obtaining redshifts should not be sensitive to the observing conditions or the Galactic latitude. Finally, in order to do large-scale structure studies, we need to be able to define a selection function, which quantifies how the galaxy population for which we have spectra depends on redshift. This allows us to make quantitative comparisons of the derived galaxy properties (such as the density field) at different distances in the sample. This in turn requires that the sample be selected on physically meaningful quantities. For this reason, we cannot simply select on the flux within the 3" aperture of the fibers, even though this would maximize the efficiency with which redshifts are measured.
With all these desiderata in mind, we plan to select our galaxy sample in the r' band using Petrosian (1976) magnitudes. We correct the photometry for the effects of Galactic extinction, using the a priori reddening map discussed in Chapter 3.7. We considered a joint selection in r' and g' , fearing that r' alone would systematically exclude blue (i.e., spiral), nearby (because of the steepness of the K-correction) galaxies. However, tests with realistic mock catalogs (Chapter 13) showed that the redshift range and morphological mix of samples selected in these two bands was quite similar; the g'-r' colors of galaxies are not a strong function of redshift (at least to the depth of our sample) or Hubble type. The u' band is of course too shallow to be useful for target selection (Chapter 8).
Define the Petrosian radius RP as that at which the ratio of azimuthally-averaged surface brightness I(r) in an annulus to the mean surface brightness within RP, falls to some specified value:
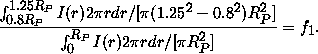
The Petrosian flux is that within a fixed number of Petrosian radii:
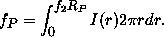
The Petrosian ratio as defined above has the drawback of being non-monotonic for some galaxies with multiple components (such as disk galaxies with prominent bulges, or active galaxies with stellar nuclei); for cD galaxies with power-law surface-brightness profiles, the Petrosian ratio becomes a constant with scale. We are still exploring algorithms to deal with these problematic cases. For f1 as small as 1/4 , the multiple component issue is rarely a problem, but we may be forced to measuring a magnitude through an aperture based on a model fit for galaxies with power-law profiles.
We need a secondary cut to minimize the number of very low-surface brightness galaxies, for which the total light down the fiber aperture is very small. We wish to avoid having a cut on the light within the 3" aperture, but rather we continue to define quantities based on the galaxy profile itself, by making a cut on the surface brightness within the circular aperture which contains half the Petrosian flux. We find that limiting in Petrosian magnitude at r' = 18.15 and Petrosian surface brightness at mur' = 22 mag arc-sec-2 yields a sample of one million galaxies over the survey area, with a sharp cutoff in the distribution of 3" aperture magnitudes at r'3" = 19.5. Moreover, the redshift distributions of spirals and ellipticals are very similar. There are some small corrections to the Petrosian magnitude and surface brightnesses, which depend on the compactness of the galaxy and the seeing, but these are straightforward to apply.
Because some fraction of the large galaxies will overlap the edges of the CCD's (Section 3.4.2), photometry of these galaxies will be unreliable, and thus we intend to augment the spectroscopic sample with all galaxies with diameters greater than 1' (the overlap between strips), independent of their Petrosian properties. The total number of galaxies affected will be quite small.
The faintest 3" limiting magnitude of 19.5 is near the point at which the contribution from the galaxy and sky in the aperture are equal; integration times would have to become substantially larger if we were to go much fainter (cf. the discussion in Section 5.3). However, there is a class of galaxies, the most luminous metal-rich red ellipticals, which have very strong absorption lines, and for which simulations show that we can go 1.5 magnitudes fainter and still measure redshift-quality spectra. We thus plan to select such galaxies by their colors and their photometric redshifts (cf., Figure 3.1.11), and target them 1.5 mag fainter than the main galaxy sample. The details are described in Section 3.2. Because these objects are luminous, they will be seen to large redshifts; we will have essentially a volume-limited sample of these objects to z ~ 0.5 with which to do large-scale structure studies on the largest scales, and to study the evolution of clusters with redshift. Moreover, because these photometric properties are those of the Brightest Cluster Galaxies (e.g., Postman and Lauer 1995, and references therein), this automatically includes all clusters with a "normal" BCG out to those redshifts (cf. the discussion in section 3.2.2.4).
The most basic statistical measures of galaxy clustering are the power spectrum and the two-point correlation function. The two quantities are a Fourier Transform pair, but estimators of the two can have quite different noise properties when applied to a finite sample, so in practice it is useful to measure them independently. With the SDSS, we can measure the angular correlation function, w( theta ) , from the photometric survey, and we can measure the redshift-space power spectrum and correlation function directly from the redshift survey. Because galaxy fluctuations are very small on the largest scales probed by the SDSS, the selection of galaxies must be exquisitely accurate to ensure that measurements are limited by statistical rather than systematic errors. Thus, the high-quality imaging survey is an absolutely essential prerequisite for the redshift survey. The photometric survey will allow galaxy selection to be precise and uniform across the survey region, much more so than for any other large scale redshift survey in existence or planned for the near future. The photometric data will also yield accurate measurements of Galactic extinction (cf. Section 3.7 and Chapter 9), which would otherwise be a debilitating source of systematic errors and limit the accuracy with which the large-scale structure could be measured.
The state of the art in measurements of the angular correlation function is the analysis of ~ 106 galaxies in the digitized, photographic, APM survey by Maddox et al. (1990; cf., Baugh and Efstathiou 1993). At large angles, the accuracy of the estimates is limited by systematic uncertainties in the Galactic extinction and photometric uniformity rather than by statistical uncertainties. The SDSS photometric survey will have 100 times as many galaxies as APM, much smaller photometric errors, and much tighter control of extinction and uniformity. It should therefore yield much more accurate measures of w( theta ) . The additional leverage of color-redshift relations (cf. Section 3.1.4) will make it possible to study the evolution of clustering in the photometric sample, especially in the Southern survey, which will go about 2 magnitudes deeper than the Northern survey.
The SDSS redshift sample, itself the size of the APM catalog, will yield precisely calibrated measures of the present-day correlation function, xi (s) , and power spectrum, P(k) , in redshift space. The SDSS will probably be the first survey with the sensitivity and freedom from systematic errors to determine unambiguously the scale at which xi (s) goes negative -- this scale provides an important constraint on theoretical models.
The power spectrum of the galaxy distribution has been measured from existing redshift surveys out to scales of about 100h-1 Mpc with approximately a factor of two precision (Vogeley et al. 1992; Fisher et al. 1993; Feldman et al. 1994; Park et al. 1994; Peacock and Dodds 1994; cf., Strauss and Willick 1995 for a review). These scales are roughly one order of magnitude smaller than the smallest scales for which the COBE satellite has measured fluctuations in the CMB (Smoot et al. 1992; Bennett et al. 1994). In the simplest interpretation, the CMB anisotropies are directly related to fluctuations in the gravitational potential (Sachs and Wolfe 1967). With the SDSS redshift survey, we will measure the galaxy power spectrum on scales where the Sachs-Wolfe effect is measurable in the CMB, and thus directly compare the amplitude of galaxy fluctuations to that of gravitational potential fluctuations.
After one year of operation, the SDSS spectroscopic sample will be an order of magnitude larger than the largest redshift surveys that exist today, and a factor of several larger than the largest redshift surveys expected to exist by that time. At the end of five years, we will measure the power spectrum over an enormous range of scales with unprecedented precision. Figure 3.1.9 shows the model power spectra for the SDSS galaxy sample and for the luminous red galaxies (cf., Section 3.2.2.4). The power spectra in Figure 3.1.9 have been computed for an Omega h = 0.25 CDM model, normalized to sigma8 = 1, with the error bars calculated for a volume limited sample in the Northern survey region. Both cosmic variance and shot noise are included in the calculation of the error bars. The power spectrum for the luminous red galaxies assumes a volume limited sample to a depth of z = 0.45. These galaxies, found preferentially in the densest regions of the Universe, are assumed to be biased by a factor of 2 with respect to the complete galaxy sample, so that the amplitude of the power spectrum is a factor of four higher than that of the galaxy sample. Both cosmic variance and shot noise are included in the estimation of error bars, but other effects, e.g. clustering evolution, are likely to dominate the uncertainties in this sample. If the model power spectrum shown in Figure 3.1.9 is a reasonable representation of the truth, we will be able to measure it beyond the turnover scale, which corresponds to the radius of the horizon at matter-radiation equality.
Also plotted in Figure 3.1.9 are the smallest comoving wavelength scales that can be observed by COBE and by the upcoming MAP (Microwave Anisotropy Probe) mission. Only SDSS can access the COBE scale; but comparison of the power spectra obtained by SDSS and other redshift surveys with the MAP data should allow the examination of structure on a very wide range of scales. The possibility of making this comparison is very exciting, for it will reveal the evolution of structure across the lifetime of the Universe.
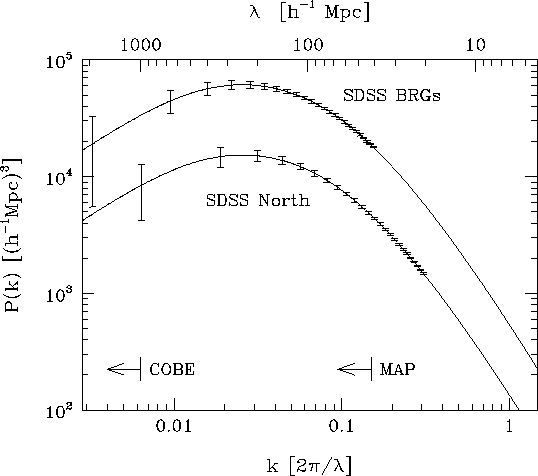
Model power spectra. The power spectra for the SDSS Northern galaxy survey and for the luminous red galaxies (BRGs) are shown. The latter are assumed to be biased by a factor of two with respect to the galaxies. The individual points and their error bars are statistically independent. On small scales, the errors are smaller than the smallest bars. Also shown are the smallest comoving wavelength scales accessible to COBE and to the upcoming Microwave Anisotropy Probe (MAP).
The detailed shape of the power spectrum reflects the physical source of the primordial fluctuations (e.g. inflation, topological defects) and the matter content of the Universe (e.g. the relative mass fractions of radiation, other relativistic components, hot dark matter, cold dark matter, baryons, and vacuum energy). Current observations are sufficient to rule out some theoretical models, such as the simplest and most attractive versions of the cold dark matter scenario. The high-precision measurements afforded by the SDSS, especially near the peak of the power spectrum, will provide much more stringent tests of theoretical models, and the ability to detect subtle features in the spectrum should allow us to ask detailed physical questions. For instance, if baryons contribute a non-negligible fraction of the cosmic mass density, then oscillations of coupled baryon-photon fluctuations produce oscillations in the power spectrum at wavelengths near the horizon radius at recombination (cf. Holtzman 1989). Measuring such oscillations would allow us to constrain Omegabaryon and to distinguish between adiabatic and isocurvature fluctuations. The high resolution we will get in k-space due to our large filled volume (cf., Figure 3.1.5) is absolutely necessary for looking for such subtle effects.
The primordial power spectrum of mass fluctuations differs from the present-day power spectrum of the galaxy distribution because of (1) non-linear gravitational effects (which are strongest on small scales), (2) distortions by peculiar velocities in redshift space (which enhance the spectrum on large scales and depress it on small scales), and (3) possible "biasing" between the galaxy and mass distributions (with unknown scale dependence). These effects complicate the comparison between theory and observation, but they are extremely interesting in their own right, and they can be explored and constrained by other statistical methods, as we discuss below.
Peculiar velocities shift galaxies along the line of sight in redshift space, creating anisotropic distortions in the correlation function and the power spectrum. On small scales, velocity dispersions stretch dense structures along the line of sight. Thus clusters of galaxies appear as "fingers-of-God" in redshift space. On large scales, coherent outflows from voids and inflows to superclusters amplify density contrasts along the line of sight (Sargent and Turner 1977; Kaiser 1987). One can recover the correlation function or power spectrum in real space by projecting over the redshift direction, but the distortions themselves are interesting, and can be quantified by measuring the correlation function or power spectrum as a function of direction with respect to the line of sight, at fixed values of the pair distance or the wavelength. From the anisotropy of the correlation function, one can extract moments of the galaxy pairwise velocity distribution (Davis and Peebles 1983; Fisher et al. 1993). These provide powerful constraints on theoretical models, particularly on the values of Omega and the "bias parameter" b , which describes the relative amplitude of galaxy and mass fluctuations. On scales in the linear regime, distortions of the correlation function or the power spectrum depend directly on the combination Omega 0.6/b (Kaiser 1987; Hamilton 1992).
With present data one can estimate Omega0.6/b with ~50% uncertainties (Hamilton 1993; Fisher et al. 1994; Cole et al. 1994, 1995; Loveday et al. 1995). The large uncertainties reflect the limited galaxy numbers and volumes of existing surveys; these add noise to the statistical estimates, and they prevent one from reaching scales that are completely in the linear regime. In particular, this technique depends on averaging over enough coherent structures of supercluster size that the sample can be considered isotropic in real space. The SDSS will be ideal for this sort of analysis -- it will provide the large number of galaxies, large survey volume, and freedom from systematic errors that are needed to measure angular modulations of low-amplitude clustering on large angular scales. From the largest, i.e., linear, scales we will obtain precise measurements of Omega 0.6/b . By examining the transition from the linear regime to the non-linear regime, we can break the degeneracy between Omega and b (Cole et al. 1995). Obtaining separate constraints on these parameters requires an enormous data set, and we expect that the SDSS will be the first redshift survey to allow an unambiguous distinction between a high density Universe with biased galaxy formation and a low-density Universe in which galaxies trace mass. We will be able to test the robustness of this distinction by applying the same analysis to galaxies of different types -- these may have different bias factors, but they should imply the same value of Omega (see Figure 3.1.9 and the discussion below on clustering of different galaxy types).
The correlation function and power spectrum measure only the rms amplitude of fluctuations as a function of scale. To obtain a complete statistical description of clustering, one must also specify the higher-order correlation functions. The careful selection criteria and dense sampling of the SDSS spectroscopic survey are designed to allow accurate measurement of higher-order clustering.
Many statistical measures are sensitive to high-order moments of the galaxy distribution, e.g. void statistics and percolation methods. Here we concentrate on the probability distribution of counts in cells (of which void statistics are a special case). White (1979) shows that the count probability distribution is given by an infinite sum over all the higher-order correlation functions; thus these two descriptions are, in principle, mathematically equivalent. Estimates of higher-order correlations and count probability distributions have been obtained from a variety of angular and redshift catalogs (e.g. Peebles and Groth 1976; Alimi et al. 1990; Meiksin et al. 1992; Maurogordato et al. 1992; Gaztañaga 1994; Bouchet et al. 1993; Szapudi, Meiksin, and Nichol 1996; cf., Strauss and Willick 1995 for a review).
On large scales, count probabilities reveal important clues about the origin of primordial density fluctuations. Simple models of inflationary cosmology predict Gaussian probability distributions in linear theory, while topological defect models (e.g. cosmic strings, texture) predict non-Gaussian fluctuations. Non-linear evolution distorts the probability distribution, but models with Gaussian initial conditions predict a specific hierarchy of relations between moments of the mass density field, at least on scales that can be treated by perturbation theory (Peebles 1980; Fry 1984; Bernardeau 1992). If the smoothed galaxy density is a local function of the smoothed mass density, then the galaxy distribution retains this hierarchy of moment relations (Fry and Gaztañaga 1993). Existing data (Gaztañaga 1992; Bouchet et al. 1993) show the expected relations for the low-order moments, but these observations probe only a modest range of length scales. The redshift and photometric samples of the SDSS will allow much more stringent tests over a large dynamic range. Even small departures from the predictions of Gaussian models would be highly significant, implying the existence of non-Gaussian primordial fluctuations, or a partial decoupling between galaxy density and mass density, which could be caused by large scale modulations in the efficiency of galaxy formation (Babul and White 1991; Bower et al. 1993; see the discussion by Frieman and Gaztañaga 1994). One could distinguish these possibilities by studying a range of physical scales and by examining galaxies of different types.
The observed galaxy distribution also exhibits hierarchical relations between higher-order correlation functions in the strongly non-linear regime. Similar behavior is seen in some numerical simulations (e.g. Bouchet et al. 1991). These relations have recently been established up to eighth order in the Lick and APM catalogs (Szapudi and Szalay 1993; Gaztañaga 1994). These scalings not only tell us about an important symmetry of the galaxy clustering, namely the validity of the (N-1) th order tree hierarchy, but also provide a quantitative measure of higher-order organization in the galaxies. The non-linear dynamics of galaxy clustering are not fully understood from first principles, and this remains an active area of research (e.g. Balian and Schaeffer 1989a; 1989b). The SDSS will significantly improve the accuracy of these measures and extend them to much higher orders, both in redshift space and projected onto the plane of the sky. It will allow a detailed examination of the transition from the perturbative to the fully non-linear regime, and it may reveal places where the hierarchical description breaks down; this information will help us understand the physical significance of the observed scaling.
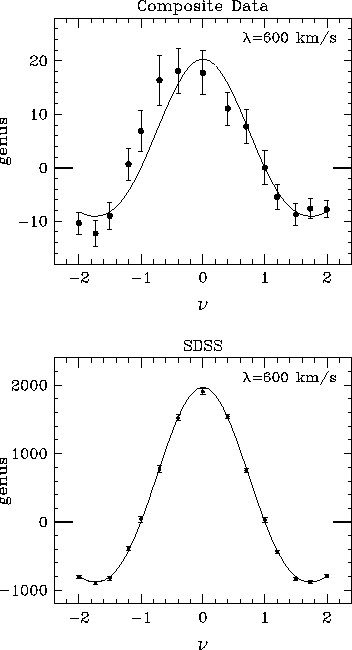
Quantitative measurement of the topology of the galaxy distribution. The upper panel, adapted from Figure 12 of Gott et al. (1989), shows the combined genus curve measured from four large, complete redshift surveys, at a smoothing length lambda =600 km s -1 . Error bars are computed by bootstrap methods. The lower panel illustrates the expected precision of genus measurements from the SDSS redshift sample. The solid curve has the universal form predicted for Gaussian density fields, with an amplitude appropriate to the SDSS survey volume assuming a standard CDM power spectrum. Points are distributed about this curve in accordance with the expected error bars, which we extrapolate from the Gott et al. sample assuming that they scale with the square-root of the number of detected structures. High-precision topology measurements will allow clear detection of small deviations from the predictions of Gaussian models.
A particularly interesting way to measure high-order clustering in the galaxy distribution is to examine the topology of high- and low-density regions. At the qualitative level, one would like to know whether the galaxy distribution is best described by a sponge topology, in which high- and low-density regions have equivalent connectivity, a bubble topology, in which voids are separated from each other by high-density walls, or a cluster topology, with isolated high-density regions residing in a low-density sea. A quantitative measure of topology is the genus curve of Gott et al. (1987), who smooth the galaxy density field and measure the genus of isodensity contour surfaces (the number of "holes" or "handles" minus the number of isolated regions), as a function of the fractional volume enclosed by the contour. The use of fractional volumes makes the topology statistic independent of the rms value and one-point distribution of the smoothed density fluctuations, so it complements the power spectrum and count probability statistics described above.
On large scales the topology is closely related to the physics of the primordial fluctuations; in particular, positive and negative fluctuations are statistically equivalent in Gaussian fields, and Gaussian models predict a specific, universal form for the genus curve. Measurements of the genus curve by Gott et al. (1989), Moore et al. (1992), and Vogeley et al. (1994) show that, to within the statistical errors, the galaxy distribution is consistent with Gaussian fluctuations on linear scales. However, none of the existing surveys includes a large enough volume to detect small deviations from the genus curve predicted for a Gaussian model. On smaller scales, Gott et al. (1989) and Vogeley et al. (1994) find departures from the Gaussian prediction, but the statistical significance of these departures is not overwhelming ( ~ 2 sigma for Vogeley et al. 1994). It is also unclear whether these these results indicate non-Gaussian initial conditions or residual effects of non-linearity and biased galaxy formation.
Because of its large volume, the SDSS redshift survey will provide a measurement of the topology on linear scales with sufficient accuracy to measure small deviations from the Gaussian prediction. The combination of this large volume with dense sampling will yield a measurement of the small scale genus curve which has a factor of ten higher signal-to-noise ratio than previous measurements (see Figure 3.1.10). Thus these topological analyses will provide tight constraints on primordial fluctuations, independent of those obtained from count probability statistics.
The above discussion touches on only a few of the possible methods to quantify galaxy clustering and test cosmological models. Many other statistics, designed to address a variety of physical questions, have been proposed for describing large scale structure (cf., Borgani 1995). These include statistics that measure the alignment of galaxies and clusters with their parent superclusters, techniques that quantify the presence of voids, sheets, and filaments, wavelet decompositions of the galaxy density field, and measurements of the fractal properties of the galaxy distribution. Reconstruction methods, wherein one works backward from the current galaxy distribution to the initial density fluctuations, provide an alternative way of addressing many of the questions posed in Section 3.1.1, complementing the purely statistical approach (Weinberg 1992; Nusser and Dekel 1993; Gramman 1993). The SDSS will provide a superb database for applying many of these techniques. We anticipate that other powerful methods will be developed over the next few years, particularly as people think about how to exploit data of the scope and quality provided by the SDSS.
One of the most exciting features of the SDSS is that we can study clustering in detail for different classes of galaxies. It is well known that the fraction of elliptical and S0 galaxies rises dramatically in the cores of rich clusters (Dressler 1980; Postman and Geller 1984; Giovanelli et al. 1986). However, it is unclear whether this morphological segregation extends to large scales, and whether it occurs outside of the densest regions. One major obstacle in addressing these issues is the small size of existing samples. Random and systematic errors in the morphological types listed by existing catalogs also pose serious problems (Santiago and Strauss 1992).
With the SDSS we can study small and large scale differences in the clustering of galaxies of different morphological types (not just spiral vs. elliptical but Sa vs. Sb, barred spiral vs. unbarred spiral, etc.), different colors, different luminosities, different surface brightnesses, and different spectroscopic properties (comparing galaxies with starburst spectra to galaxies with old-population spectra, AGN galaxies to "normal" galaxies, and so on). The SDSS photometric sample will be cross-correlated with samples from large-angle surveys in other bands, e.g. X-rays from the ROSAT all-sky survey, near-infrared from the Two-Micron All Sky Survey (2MASS; cf., Kleinmann 1992), far-infrared from IRAS, and radio from the VLA B Array survey at 20 cm (Becker, White, and Helfand 1995) (cf. Section 3.8). We can therefore compare the clustering of garden-variety optical galaxies to that of galaxies that are bright in these various bands. In addition, the SDSS spectroscopic sample will go appreciably deeper than the 2MASS survey, allowing us to define the 2MASS galaxy selection function exquisitely well over the Northern Galactic Cap. This is a necessary ingredient in calculating the angular dipole moment of the (full-sky) 2MASS galaxy sample (cf. Villumsen and Strauss 1987). This dipole moment can be compared with the 600 km/s motion of the Local Group relative to the rest frame of the Cosmic Microwave Background in order to determine Omega0 (cf., Strauss and Willick 1995).
Two features of the SDSS make it uniquely suited to such studies: the accurate photometric fluxes, high-resolution images, and high signal-to-noise spectra allow us to divide galaxies into classes objectively and with small errors, and the full galaxy sample is large enough that we can take even rather specialized subdivisions and still measure clustering accurately over a wide range of scales. No other planned redshift survey will match these capabilities.
Clustering studies divided by galaxy type will be particularly valuable for addressing the second category of questions introduced in Section 3.1.1. They will provide important clues about the physical processes that influence galaxy formation and determine galaxy properties. They will also provide crucial information about the relation between the galaxy and mass distributions, thereby helping to separate effects of biased galaxy formation from signatures of primordial fluctuations and cosmological parameters (particularly Omega ). As a single example, suppose that we measure correlation functions for several different galaxy types at large scales. If all of these correlation functions have the same shape (perhaps with different amplitudes), we will have excellent reason to believe that this is also the shape of the mass correlation function, and hence a direct constraint on the primordial fluctuations. If the shape varies from one type to another, on the other hand, we might conclude that galaxy formation has been influenced by some long-range process (e.g. Bower et al. 1993), and that the true shape of the mass correlation function remains uncertain.
Given the resolution of the spectrograph, to what depth and accuracy can peculiar velocities be measured? With a resolving power of ~ 2000 the velocity resolution is ~ 150 km/s. As each resolution element is sampled by 3 pixels, velocity dispersions and linewidths can be fitted to an accuracy of 10-20 km/s for high signal-to-noise ratio data. With these data, distances can be derived from the Dn-sigma (Dressler et al. 1987), Tully-Fisher (e.g., Pierce and Tully 1988), and Brightest Cluster Galaxy (BCG; Hoessel 1980; Lauer and Postman 1994) relations. The simulations of galaxy spectra in Figure 3.4.2 indicate that velocity dispersions can be measured for elliptical galaxies to r'=17 and linewidths for spiral galaxies to r'=17.5 . A further limitation applies to the Tully-Fisher relation. While H alpha rotation curves give Tully-Fisher distances as accurate as those from HI linewidths (Courteau 1992), the data we obtain will be from fiber, not slit spectroscopy. For an H alpha linewidth to be meaningful the rotation curve must turn over within the diameter of the fiber. Typically this occurs at 2-3 kpc (from the data of Courteau 1992). Therefore, we will be able to apply the Tully-Fisher relation only for z>0.05 , which is the outer limit of existing velocity-field surveys. For more nearby spirals, one can supplement the SDSS multi-color photometry with independent measures of optical or HI linewidths. There exists a distance indicator for BCGs which depends on photometric measurements only (Lauer and Postman 1994), so if one can compensate for the effects of seeing one can measure their distances even without spectroscopic information.
Distance errors of 15% are typical for each of these distance estimators. Assuming a median redshift of z=0.1 (the sample for which we can measure Dn - sigma distances will be shallower than this, and the Tully-Fisher and BCG samples deeper), the velocity error on an individual galaxy is 4500 km/s. To reduce the error on these velocities and, therefore, detect the signature of the velocity field, we can bin the data in 50 h-1 Mpc cells, each containing ~ 400 galaxies suitable for Tully-Fisher measurements, allowing us to reduce the errors to 200 km/s per volume. In overdense regions and at lower redshift (as the error per galaxy decreases and the number density of galaxies in the sample increases) we can decrease the cell size dramatically. We estimate that we will obtain over 300 independent, statistically significant measures of the velocity field across the full SDSS survey volume.
Because the SDSS has a large opening angle, the measured peculiar velocity field will be sensitive to the bulk motions detected by existing surveys (Mathewson et al. 1992; Courteau et al. 1993; Lauer and Postman 1994), and to the convergence of these flows towards the CMB rest-frame. Analyses in radial shells will be able to detect the scale at which convergence occurs. The rate of convergence and the amplitude of the velocity field binned on large scales provide direct constraints on long-wavelength modes of the mass power spectrum.
Using the peculiar velocity field within the survey volume, we can apply the reconstruction techniques of Dekel et al. (1990) and Ganon and Hoffman (1993) to determine the mass-density field for the volume surveyed. Comparison between the galaxy number densities and mass density derived from the velocities yields a direct measure of the cosmological density parameter and the bias, in the combination Omega 0.6/b (cf. Dekel et al. 1993), a measure that is independent of that obtained from the anisotropy of clustering in redshift space discussed in Section 3.1.3. The peculiar velocity approach will also require measuring the galaxy density fluctuations on scales comparable to the smoothing of the velocity field, but the uniformity and high sampling density of the redshift survey will make this possible.
A major strength of this data set is the existence of a fully sampled redshift survey containing the same galaxies from which the peculiar velocity data are obtained. Existing studies of peculiar velocities are limited by an incomplete understanding of the biases inherent in proper distance measurements, such as Malmquist bias. As reviewed by Strauss and Willick (1995), convolution of the dispersion in the distance indicator with the real distribution of galaxies leads to spurious components in the velocity field. From the complete redshift survey we will know the number density distribution of galaxies and the selection function used in deriving the velocity field samples. Thus we can correct the peculiar velocity data for these biases in a self-consistent way.
We may even be able to use the redshift-distance relation to put constraints on the curvature of the Universe q0. The expected effects will be small, but no smaller than those we are trying to measure to get a handle on peculiar velocities. However, as Fisher et al. (1992) show, curvature effects and those due to galaxy evolution are expected to be comparable even at low redshifts, and detailed modeling of the colors and spectra will be necessary to disentangle these effects. Evolutionary effects will also have to be taken into account when measuring the peculiar velocities at z ~ 0.1 .
The discussion here is based on our current understanding of the properties of distance indicators. In the local Universe, the effects of environment, density, and morphology on distance indicators are poorly understood (Bottinelli et al. 1982; Silk 1989). The SDSS will be a superb data set with which to study these questions, since it provides spectroscopy and multi-color photometry for a large sample of galaxies. The results will have important implications for peculiar velocity measurements with the SDSS and for existing peculiar velocity surveys. Correlating with the distance-independent parameters available from the photometric data may lead to improvements in the distance indicators (Connolly 1993), or to completely new redshift-independent measures of distance.
While the SDSS galaxy redshift survey will be complete to r'~18.1 , the photometric data extend 5 magnitudes deeper for the Northern sample and 7 magnitudes deeper for the Southern strip. We can substantially increase the power of the SDSS by deriving approximate galaxy redshifts from the broad-band colors. Photometric redshifts are accurate enough for basic measures of the evolution of the galaxy population and of galaxy clustering. Deriving approximate redshifts to the limit of the photometric survey will increase the number of objects available for study of the spatial distribution of galaxies from 10 6 to 5 x 107.
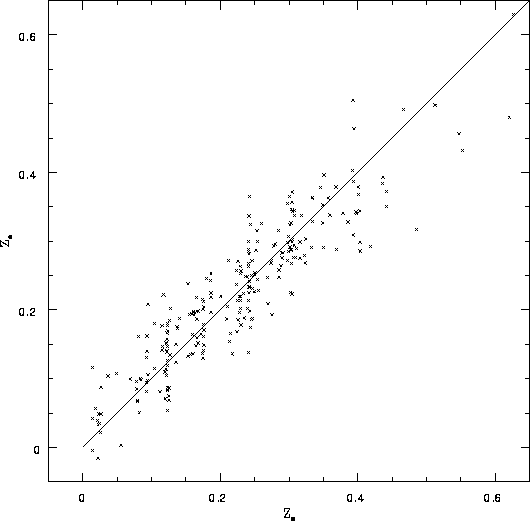
Estimating redshifts from photometry. The figure shows the estimated redshift vs. the spectroscopic redshift for the Koo and Kron UJFN photographic data, to BJ = 22.5 . The formal dispersion is Delta z =0.047 , largely dominated by photometric errors. The underestimate of galaxy redshifts at faint magnitudes is due to Malmquist bias. From Connolly et al. (1995).
Deep multi-color photographic data in the selected areas SA57 and SA68 (cf. Koo and Kron 1992) have shown that the distribution of galaxies in the four-color space U, BJ , RF, IN is almost planar (Connolly et al. 1995). In this plane, lines of constant redshift and lines that trace the luminosity evolution of galaxy spectral types are almost orthogonal. The dispersion in the color-redshift relation is Delta z = 0.047 to BJ=22.5 (Figure 3.1.11), where the scatter is already dominated by photometric errors. We have modeled the relation given the signal-to-noise ratio of the SDSS and find that the dispersion reduces to Delta z=0.02 for z < 1 , especially for the reddest galaxies (cf. Section 3.2.2.4). The photometric survey of the Southern strip will yield many galaxies at z>~ 1 .
Calibration of the color-redshift relation requires a homogeneous sample of galaxies with spectroscopic redshifts that covers the magnitude and redshift range of the photometric survey. For r'<18.1 the complete distribution of galaxies in color space is determined from the SDSS spectroscopic survey. One can extrapolate to higher redshifts by simply applying K-corrections to the galaxy colors, but it is far better to calibrate the color-redshift relation directly with faint galaxy redshift surveys, which currently extend to B=24 (e.g. Glazebrook et al. 1995). These data will be superseded by the Keck DEEP redshift survey (Mould 1993; cf. Appendix A), which will obtain 20,000 redshifts to a depth of B=25.5 .
Given a sample size of N ~ 5 x 107 with distances accurate to Delta z = 0.02 , we can study the evolution of the galaxy luminosity function and the galaxy correlation function with unprecedented accuracy. The latter will be particularly interesting given recent results (Efstathiou et al. 1991) implying that the faint blue population shows anomalously weak clustering, perhaps implying that this is a quite distinct population. The Southern survey, in particular, will go deep enough to address these issues. The results of these analyses will allow us to test predictions of a wide range of galaxy formation theories, including detailed scenarios like standard cold dark matter and more phenomenological models involving mergers or interactions.
In an optical survey like the SDSS, galaxies provide the basic markers of large scale structure. Nonetheless, it is useful to group galaxies into clusters and superclusters, and to consider these objects as entities in themselves, for several reasons. First, clusters allow one to trace structure to larger scales and higher redshifts, even without a complete galaxy redshift sample, via the cluster-cluster correlation function and similar measures. Second, it is interesting to study the properties of galaxies in cluster and supercluster environments, especially at high redshifts. Finally, the properties of clusters and superclusters, and the evolution of these properties, themselves provide important constraints on theories of structure formation. For example, cluster mass-to-light ratios and the distribution of cluster velocity dispersions depend strongly on the amplitude of mass fluctuations and the values of Omega and b . Substructure and evolution of cluster properties are expected to be strong in Omega =1 cosmologies and weaker in open cosmologies.
For several decades, studies of clusters and superclusters have relied heavily on Abell's (1958) catalog, based on visual examination of photographic plates. Abell identified clusters by counting galaxies within a specified magnitude range and metric radius. Recent cluster catalogs based on visual examination (Abell, Corwin, and Olowin 1989) and digitized Schmidt plates (Dodd and MacGillivray 1986; Dalton et al. 1992) have used variants of Abell's criterion.
The SDSS galaxy redshift catalog will have a median depth similar to that of the Abell cluster catalog. Within this volume, we can identify clusters using complete redshift-space information, greatly reducing contamination effects. We will obtain dozens or even hundreds of galaxy redshifts in these clusters, allowing accurate measures of cluster properties. State-of-the-art algorithms for identifying clusters from photometric data use matched filters in position-magnitude space (Postman et al. 1995). The SDSS photometric survey will provide a superb database for application of such techniques. Multi-color photometry will be extremely useful here, as it provides redshift information that can be used to reduce contamination from foreground and background galaxies (cf. the previous subsection). We can improve cluster identification in both the redshift and photometric catalogs by using color and morphology data to select early-type galaxies, which are much more common in cluster cores than in the field. This approach will be especially important at high redshifts, where every reduction in contamination greatly increases sensitivity. As discussed earlier and in Section 3.2.2.4, we plan to identify the most luminous red ellipticals, and target them for spectroscopy 1.5 mag fainter than the main galaxy survey, taking advantage of the fact that they tend to have complex spectra with strong absorption lines. This sample will include the majority of brightest cluster galaxies, and in this way, we will obtain a cluster redshift survey that extends to much greater depth than the galaxy redshift survey, at almost no cost in fibers. The high-redshift clusters will be interesting targets for follow-up observations with other telescopes, and we will want to correlate the SDSS cluster catalog with the Abell catalog and ROSAT and other X-ray surveys. Further aspects of cluster science are discussed in Section 3.2.
To date, most catalogs of superclusters have been created by applying some sort of percolation algorithm to a cluster catalog (Huchra and Geller 1982; Bahcall and Burgett 1986). The depth and high sampling density of the SDSS will allow us to identify superclusters directly from the galaxy redshift survey, using objective techniques. We can, for instance, apply Bayesian reasoning to the problem of identifying groups of cells that lie above overdensity thresholds in redshift space. Initially, we wish to classify cells as lying above or below the threshold, and given the local sampling rate (a function of distance), we can find the optimal threshold so that the ratio of erroneous classifications to correct classifications is minimized. We can then account for correlations between nearby cells using an iterative algorithm in which neighboring cells "interact" with a strength proportional to the correlation, pulling anomalous low-density cells in a high-density environment up, and vice versa. Small fluctuations are suppressed, and when the procedure reaches a steady state one is left with coherent groups of cells that represent superclusters. The whole operation can be repeated for various thresholds. Thus we obtain an optimal reconstruction of the largest scale coherent structures.
The QSO redshift survey will allow us to probe clustering over enormous length scales and at high redshifts. The formation epoch of the first quasars, the evolution of the quasar luminosity function, and the clustering of quasars provide important tests for theories of structure formation (e.g. Efstathiou and Rees 1988; Turner 1991). These and other aspects of quasar science are discussed in Section 3.3.
From the point of view of large scale structure, one of the most exciting by-products of the QSO survey will be an enormous catalog of absorption line systems, both metal-line absorbers and Lyman alpha clouds. In effect, each QSO provides its own pencil-beam redshift survey of absorbers. Unlike a flux-limited galaxy catalog, the selection function for finding absorbers does not drop rapidly with redshift; in fact it increases, making absorbers excellent markers for the analysis of structure at high redshift (Crotts et al. 1995; Quashnock et al. 1996).
The interpretation of absorption line clustering is somewhat more complicated than that of galaxy clustering, since the number density of absorbers can be affected by the local state of the intergalactic medium (IGM) and by fluctuations in the metagalactic radiation field as well as by underlying fluctuations in the mass density. Despite the wealth of observational data on Lyman alpha absorbers, their precise nature and formation mechanism remain uncertain; several models have been proposed (e.g. Ikeuchi and Ostriker 1986; York et al. 1986; Bond et al. 1988; Rees 1986; Hernquist et al. 1996). The continuity of HI column densities up to and beyond 1017cm -2 suggests that the clouds extend in mass all the way up to Lyman-limit systems (Tytler 1987) and damped systems (Wolfe 1983), which are often thought to be related to forming galaxies. However, clustering in the Lyman alpha forest appears to be quite weak at high redshifts. It is not clear whether this reflects strong evolution of clustering in the mass distribution, or whether it just indicates that the clouds are less strongly clustered than the mass. Recent results find weak clustering signals in the Lyman alpha forest (Kulkarni et al. 1995; Songaila and Cowie 1996), favoring the former explanation (Lanzetta et al. 1995; Zhang et al. 1995, 1996).
Improved data on absorbers at high and low redshifts, and the increasing power of cosmological simulations with gas dynamics, should help resolve these questions over the next few years. We anticipate that clustering of absorption lines will become one of the testable predictions of theories of structure formation and models of the IGM, a particularly important prediction because it applies to the high-redshift Universe. The SDSS sample of absorption line systems will be unique, 1000 times larger than anything in existence today (see Section 3.3.4.4). The quasar survey will probe over 100,000 pencil beams, whose lengths are determined by the redshifts of the quasars and by the locations of Lyman-limit systems that block part of the continuum. These pencil beams fill, sparsely but quite uniformly, a volume whose linear dimension is measured in Gpc. The statistical noise will be extremely small, enabling us to detect even weak clustering. The high density of beams will allow us to measure the power spectrum using pairs of objects on separate lines of sight, thus obtaining a well-behaved window function (Szalay et al. 1991); this approach offers substantial advantages over clustering analyses that only consider absorbers along the same line of sight. The resolution of the SDSS spectrographs will not be as high as that of some other absorption line studies, making identification of weaker Lyman alpha lines difficult. Press et al. (1993) and Zuo and Bond (1993) propose correlating the quasar spectra in the flux regime before any lines are identified, which will largely circumvent this problem. Cosmological simulations like those of Cen et al. (1994), Zhang et al. (1995) and Hernquist et al. (1996) can yield theoretical predictions for flux distributions and correlations incorporating instrumental resolution and noise, thus allowing direct comparison to the immense data base that the SDSS quasar spectra will provide. This type of analysis will result in an accurate picture of large scale structure at high redshift (z = 1.5 to 5), complementing photometric redshifts in this régime (Lanzetta et al. 1996).
Galaxy redshift surveys have provided spectacular maps of the large scale galaxy distribution and taught us a great deal about structure in the Universe. They have stimulated, and begun to answer, the questions with which we introduced this chapter. New redshift surveys, some ongoing, some planned for the future, will extend our knowledge to larger scales, and they will complement the SDSS redshift survey in important ways, by probing structure at higher redshifts and by providing maps of the nearby galaxy distribution that cover the whole sky.
The SDSS will make an exceptionally powerful contribution to the study of large scale structure because of its size, its uniformity, and the high quality of its photometric and spectroscopic data. These will allow galaxy clustering in the present-day Universe to be measured with unprecedented precision and detail. As we have emphasized throughout this section, precision and detail are the keys to addressing important physical questions, whether constraining the matter content from subtle features near the peak of the power spectrum, determining Omega from the anisotropy of clustering in redshift space, searching for small departures from Gaussian initial conditions to identify the physical origin of primordial fluctuations, or comparing clustering of different galaxy types to test models of biased galaxy formation. The design of the SDSS has to a large extent been motivated by these questions, and specifically by the goal of measuring galaxy clustering via the statistical methods described in Section 3.1.3. Other investigations, like measurements of large scale peculiar velocities or photometric redshifts, are possible because of the resulting, general purpose design. The breadth and quality of the SDSS data make it capable of addressing a wide range of questions about large scale structure, including questions we have not yet thought to ask. They also make it a powerful database for addressing many other astronomical issues, as discussed in the remainder of this chapter.
Abell, G.O. 1958, ApJSuppl 3, 211.
Abell, G.O., Corwin, H.G., and Olowin, R.P. 1989, ApJSuppl 70, 1.
Alimi, J.-M., Blanchard, A., and Schaeffer, R. 1990, ApJL 349, 5.
Babul, A., and White, S.D. M. 1991, MNRAS 253, 31P.
Bahcall, N.A., and Burgett, W.S. 1986, ApJL 300, 35.
Balian, R., and Schaeffer, R. 1989a, AstrAp 220, 1.
Balian, R., and Schaeffer, R. 1989b, AstrAp 226, 373.
Baugh, C. M., and Efstathiou, G. 1993, MNRAS 265, 145.
Becker, R.H., White, R.L., and Helfand, D.J. 1995, ApJ 450, 559.
Bennett, C.L. et al. 1994, ApJ 436, 423.
Bernardeau, F. 1992, ApJ 392, 1.
Bond, J.R., Szalay, A.S., and Silk, J. 1988, ApJ 324, 627.
Borgani, S. 1995, Phys. Rep., 251, 1.
Bottinelli, L., Gouguenheim, L., and Paturel, G., 1982, AstrAp 113, 61.
Bouchet, F.R., Schaeffer, R., and Davis, M. 1991, ApJ 383, 19.
Bouchet, F.R., Strauss, M.A., Davis, M., Fisher, K.B., Yahil, A., and Huchra, J.P. 1993, ApJ 417, 36.
Bower, R. G., Coles, P., Frenk, C.S., White, S.D.M. 1993, ApJ 405, 403.
Broadhurst, T.J., Ellis, R.S., Koo, D.C., and Szalay, A.S. 1990, Nature 343, 726.
Cen, R., Miralda-Escudé, J., Ostriker, J.P., and Rauch, M. 1994, ApJL 437, 9.
Cole, S., Fisher, K.B., and Weinberg, D.H. 1994, MNRAS 267, 785.
Cole, S., Fisher, K.B., and Weinberg, D.H. 1995, MNRAS 275, 515.
Colombi, S., Bouchet, F. R., and Schaeffer, R. 1994, AstrAp 281, 301.
Colombi, S., Bouchet, F. R., and Schaeffer, R. 1995, ApJSuppl 96, 401.
Connolly, A.J. 1993, Ph.D. Thesis, University of London.
Connolly, A.J., Csabai, I., Szalay, A.S., Koo, D.C., Kron, R.G., and Munn, J.A. 1995, AJ 110, 2655.
Courteau, S. 1992, PhD. Thesis, University of California, Santa Cruz.
Courteau, S., Faber, S.M., Dressler, A., and Willick, J. 1993, ApJL 412, 51.
da Costa, L. N., Pellegrini, P., Sargent, W., Tonry, J., Davis, M., Meiksin, A., Latham D., Menzies, J., and Coulson, I. 1988, ApJ 327, 544.
da Costa, L. N., Vogeley, M. S., Geller, M. J., Huchra, J. P., and Park, C. 1994, ApJL 437, 1.
Crotts, A.P.S., Melott, A.L., York, D.G., and Fry, J.N. 1995, Phys. Lett. B, 155B, 251.
Dalton, G.B., Efstathiou, G., Maddox, S.J., and Sutherland, W.J. 1992, ApJL 390, 1.
Davis, M., and Peebles, P.J.E. 1983, ApJ 267, 465.
Dekel, A., Bertschinger, E., and Faber, S. M. 1990, ApJ 364, 349.
Dekel, A., Bertschinger, E., Yahil, A., Strauss, M., Davis, M., and Huchra, J. 1993, ApJ 412, 1.
de Lapparent, V., Geller, M.J., and Huchra, J.P. 1986, ApJL 302, 1.
de Lapparent, V., Geller, M.J., and Huchra, J.P. 1991, ApJ 369, 273.
Dodd, R.J., and MacGillivray, H.T. 1986, AJ 92, 706.
Dressler, A. 1980, ApJ 236, 351.
Dressler, A., Faber, S.M., Burstein, D., Davies, R.L., Lynden-Bell, D., Terlevich, R.J., and Wegner, G. 1987, ApJ 313, L37.
Efstathiou, G., Bernstein, G., Katz, N., Tyson, J.A., and Guhathakurta, P. 1991, ApJL 380, 47.
Efstathiou, G. and Rees, M.J. 1988, MNRAS 230, 5P.
Feldman, H., Kaiser, N., and Peacock, J. 1994, ApJ 426, 23.
Fisher, K.B., Strauss, M.A., Davis, M., Yahil, A., and Huchra, J.P. 1992, ApJ 389, 188.
Fisher, K.B., Davis, M., Strauss, M.A., Yahil, A., and Huchra, J.P. 1993, ApJ 402, 42.
Fisher, K.B., Davis, M., Strauss, M.A., Yahil, A., and Huchra, J.P. 1994, MNRAS 267, 927.
Fisher, K. B., Huchra, J. P., Davis, M., Strauss, M. A., Yahil, A., and Schlegel, D. 1995, ApJSuppl, 100, 69.
Frieman, J., and Gaztañaga, E. 1994, ApJ 425, 392.
Fry, J.N. 1984, ApJ 279, 499.
Fry, J.N., and Gaztañaga, E. 1993, ApJ 413, 447.
Ganon, G. and Hoffman, Y. 1993, ApJL 415, 5.
Gaztañaga, E. 1992, ApJL 398, 17.
Gaztañaga, E. 1994, MNRAS 269, 913.
Geller, M.J., and Huchra, J.P. 1989, Science 246, 897.
Giovanelli, R., Haynes, M.P., and Chincarini, G. 1986, ApJ 300, 77.
Glazebrook, K., Ellis, R., Colless, M., Broadhurst, T., Allington-Smith, J., and Tanvir, N. 1995, MNRAS 273, 157.
Gott, J.R., Weinberg, D.H., and Melott, A.L. 1987, ApJ 306, 341.
Gott, J.R., et al. 1989, ApJ 340, 625.
Gramann, M. 1993, ApJ 405, 449.
Hamilton, A.J.S. 1992, ApJL 385, 5.
Hamilton, A.J.S. 1993, ApJL 406, 47.
Hernquist, L., Katz, N., Weinberg, D.H., and Miralda-Escudé, J. 1996, ApJL 457, 51.
Hoessel, J.G. 1980, ApJ 241, 493.
Holtzman, J.A. 1989, ApJSuppl 71, 1.
Huchra, J., Davis, M., Latham, D., and Tonry, J. 1983, ApJSuppl 52, 89.
Huchra, J. and Geller, M.J. 1982, ApJ 257, 423.
Ikeuchi, S., and Ostriker, J.P. 1986, ApJ 301, 522.
Kaiser, N. 1986, MNRAS 219, 785.
Kaiser, N. 1987, MNRAS 227, 1.
Kaiser, N., and Peacock, J.A. 1991, ApJ 379, 482.
Kirshner, R.P., Oemler, A., Schechter, P.L., and Shectman, S.A. 1981, ApJL 248, 57.
Kleinmann, S. G. 1992, in Robotic Telescopes for the 1990's, edited by A. Filippenko, ASP Conference Series, 34 (San Francisco: Astronomical Society of the Pacific), 203.
Koo, D., and Kron, R. 1992, AnnRevAAp 30, 613.
Kulkarni, V., Huang, K.-L., Green, R.F., Bechtold, J., Welty, D., and York, D.G. 1996, MNRAS 279, 218.
Landy, D.S., Shectman, S.A., Lin, H., Kirshner, R.P., Oemler, A.A., and Tucker, D. 1996, ApJL 456, 1.
Lanzetta, K.M., Bowen, D.V., Tytler, D., and Webb, J.K. 1995, ApJ 442, 538.
Lanzetta, K.M., Yahil, A., and Fernandez-Soto, A. 1996, Nature 381, 97.
Lauer, T., and Postman, M. 1994, ApJ 425, 418.
Lawrence, A. et al. 1995, in preparation.
Loveday, J., Efstathiou, G., Peterson, B., A., and Maddox, S. J. 1992, ApJ 400, 43.
Loveday, J., Maddox, S. J., Efstathiou, G., and Peterson, P. A. 1995, ApJ 442, 457.
Maddox, S.J., Efstathiou, G., Sutherland, W.J., and Loveday, J. 1990, MNRAS 242, 43P.
Mathewson, D.S., Ford, V.L., and Buchhorn, M. 1992, ApJL 389, 5.
Maurogordato, S., Schaeffer, R., and da Costa, L.N. 1992, ApJ 390, 17.
Meiksin, A., Szapudi, I., and Szalay, A. 1992, ApJ 394, 87.
Moore, B., Frenk, C., Weinberg, D., Saunders, W., Lawrence, A., Rowan-Robinson, M., Kaiser, N., Efstathiou, G., and Ellis, R.S. 1992, MNRAS 256, 477.
Mould, J.R. 1993, ASP Conference Series 43, 281.
Nusser, A., and Dekel, A. 1993, ApJ 405, 437.
Park, C., Vogeley, M.S., Geller, M.J., and Huchra, J.P. 1994, ApJ 431, 569.
Peacock, J. A., and Dodds, S. J. 1994, MNRAS 267, 1020.
Peebles, P.J.E. 1980, The Large Scale Structure of the Universe (Princeton: Princeton University Press).
Peebles, P.J.E., and Groth, E.J. 1976, AstrAp 531, 31.
Petrosian, V. 1976, ApJL 209, 1.
Pierce, M.J., and Tully, R.B. 1988, ApJ 330, 579.
Postman, M.P. and Geller, M.J. 1984, ApJ 281, 95.
Postman, M.P., Lubin, L., Gunn, J.E., Oke, J.B., Hoessel, J.G., Schneider, D.P., and Christensen, J.A. 1995, AJ 111, 615.
Postman, M.P., and Lauer, T.R. 1995, ApJ 440, 28.
Press, W.H., Rybicki, G.B., and Schneider, D.P. 1993, ApJ 414, 64.
Quashnock, J., VandenBerk, D.E., and York, D.G. 1996, ApJL 472, 69.
Ramella, M., Geller, M.J., and Huchra, J.P. 1990, ApJ 353, 51.
Rees, M.J. 1986, MNRAS 218, 25p.
Sachs, R.K., and Wolfe, A.M. 1967, ApJ 147, 73.
Santiago, B.X., and Strauss, M.A. 1992, ApJ 387, 9.
Santiago, B. X., Strauss, M. A., Lahav, O., Davis, M., Dressler, A., and Huchra, J. P. 1996, ApJ 461, 38.
Sargent, W.W., and Turner, E.L. 1977, ApJL 212, 3.
Saunders, W., Frenk, C. S., Rowan-Robinson, M., Efstathiou, G., Lawrence, A., Kaiser, N., Ellis, R. S., Crawford, J., Xia, X.-Y., and Parry, I. 1991, Nature 349, 32.
Shectman, S.A., Landy, S.D., Oemler, A., Tucker, D.L., Lin, H., Kirshner, R.P., and Schechter, P.L. 1996, ApJ 470, 172.
Silk, J. 1989, ApJL 345, 1.
Smoot, G.F., Bennett, C.L., Kogut, A., Wright, E.L., Aymon, J., Boggess, N.W., Cheng, E.S., De Amici, G., Gulkis, S., and Hauser, M.G. 1992, ApJL 396, 1.
Songaila, A., and Cowie, L. 1996, AJ 112, 335.
Strauss, M.A., Huchra, J.P., Davis, M., Yahil, A., Fisher, K.B., and Tonry, J.P. 1992, ApJSuppl 83, 29.
Strauss, M.A. and Willick, J.A. 1995, Physics Reports, 261, 271.
Szalay, A.S., Broadhurst, T.J., Ellman, N., Koo, D.C., and Ellis, R. 1991, Proc. Natl. Acad. Sci., 90, 4858.
Szapudi, I., Meiksin, A., and Nichol, R.C. 1996, ApJ 473, 15.
Szapudi, I., and Szalay, A. 1993, ApJ 408, 43.
Szapudi, I., and Szalay, A. 1996, ApJ 459, 504.
Tegmark, M. 1995, ApJ 455, 429.
Turner, E.L. 1991, AJ 101, 5.
Tytler, D. 1987, ApJ 321, 49.
Villumsen, J. V., and Strauss, M. A. 1987, ApJ 322, 37.
Vogeley, M.S., Park, C., Geller, M.J., Huchra, J.P., 1992, ApJL 391, 5.
Vogeley, M.S., Park, C., Geller, M.J., Huchra, J.P., and Gott, J.R. 1994, ApJ 420, 525.
Weinberg, D.H. 1992, MNRAS 254, 315.
White, S.D.M. 1979, MNRAS 186, 145.
Wolfe, A.M, 1983, ApJL 268, 1.
York, D.G., Dopita, M., Green, R.F., and Bechtold, J. 1986, ApJ 311, 610.
Zhang, Y., Anninos, P., and Norman, M.L. 1995, ApJL 453, 57.
Zhang, Y., Meiksin, A., and Norman, M.L. 1996, Ap. J. in press.
Zuo, L., and Bond, J.R. 1994, ApJ 423, 73.